Blog

O gravitační teorii bylo napsáno mnoho, proto zde zmíníme pouze nejvýznamnější události. První vědecký popis gravitace formuloval Isaac Newton. Na otázku, co je podstatou gravitace, jak a proč vzniká, nám žádnou odpověď neposkytl.

Vysvětlení této otázky nám o něco později naznačil Albert Einstein v Obecné teorii relativity. Výraz „časoprostor“ začal být běžně používán a Albert Einstein prohlásil, že přítomnost hmoty ovlivňuje jeho zakřivení. Toto zakřivení nazval gravitací. Vysvětlil, že čím je těleso hmotnější, tím více zakřivuje časoprostor ve svém okolí a z tohoto důvodu také roste přitažlivá síla tohoto tělesa. Poukázal na podobnost gravitační síly a síly setrvačné. Poté, co se jeho myšlenky staly obecně přijatelné pro širokou akademickou obec i laickou veřejnost, začalo se objevovat velké množství obrázků, které tuto vlastnost graficky znázorňovaly.

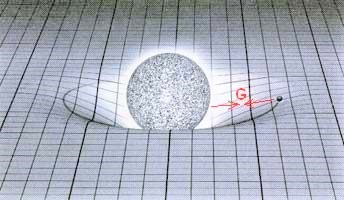
Obr. 1 – časoprostor je zde „ochuzen“ o třetí dimenzi a je znázorněn jako dvourozměrná pružná membrána, na kterou se my, jako pozorovatelé, díváme odněkud ze čtvrtého prostorového rozměru.

Omlouvám se autorovi obrázku č.1, že jsem jeho výtvor použil bez jeho souhlasu. Časoprostor je zde nakreslen jako pružná blána s mřížkou černých čar, abychom byli lépe schopni vidět jeho zakřivení. Hmotné těleso, znázorněné velkou koulí, je zobrazeno jakoby mimo tento časoprostor, ale to pouze z důvodu snazšího pochopení. Ve skutečnosti je toto těleso jeho součástí a mělo by být nakresleno jako kruh na ploše časoprostoru.

Tento objekt se v důsledku vlastní hmotnosti „boří“ do časoprostoru a vytváří v něm jakýsi důlek. To je to zakřivení o kterém hovořil v souvislosti s obecnou teorií relativity Albert Einstein. Tento důlek je tím větší, čím hmotnější je znázorněné těleso. Dále je na tomto obrázku ještě další, mnohem menší těleso, které také vytváří v prostoru svůj vlastní důlek, ale menší, úměrně k jeho hmotnosti. Z toho všeho vyplývá jednoduchý předpoklad, že tato tělesa jsou vlivem svých důlků k sobě nezadržitelně přitahována, jako že se to menší těleso skutálí do důlku toho většího. Asi stejně jako kuličky, kdybychom je položili na gumovou blánu. Zbývá již jen domalovat několik fotonů, které proletí v těsné blízkosti velkého tělesa a vlivem „důlků“ svoji přímou dráhu ohnou směrem k hmotnému tělesu.

Vzhledem ke skutečnosti, že toto bylo mnohokrát pozorováno a matematicky spočítáno, berme tyto informace jako prokázané. Znovu opakuji, že „důlky“ v prostoru kolem hmotných těles znázorňují zakřivení časoprostoru, které Albert Einstein (a po něm i všichni ostatní) nazývá gravitace. Na internetu najde zvídavý čtenář stovky stejných nebo podobných vyobrazení. Autoři se předhánějí, kdo nakreslí hlubší trychtýř a ihned po objevu černých děr začali malovat důlky opravdu velmi hluboké. Ti nejodvážnější přišli s myšlenkou, že časoprostor je nejen velice pružný, ale že ho lze dokonce přetrhnout a znovu spojit a vymysleli pojem červí díra. Za zmínku ještě stojí i názor příznivců všemožných symetrií, kteří věří, že pokud existuje černá díra, tak logicky někde bude i díra bílá, neboť v přírodě je přece vše symetrické. Ale neodbíhejme od tématu. Použitelné informace jsou následující: časoprostor je pružný, hmota jej zakřivuje a zakřivení časoprostoru (neboli gravitace) ovlivňuje hmotu.

Pro jednodušší grafické znázorňování popisovaných vlastností časoprostoru a hmotných těles (a také proto, abych nemusel krást cizí obrázky), budu kreslit trojrozměrný časoprostor jako jednorozměrnou čáru. Takže horní obrázek bude v mém zjednodušeném podání vypadat takto:

        
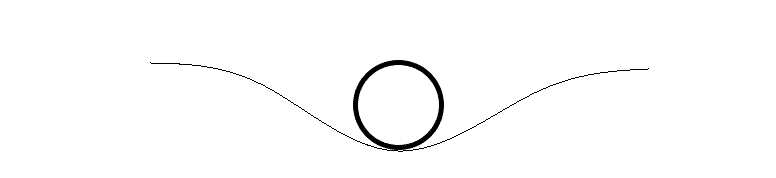
Obr. 2 – náš trojrozměrný prostor je zde „ochuzen“ o druhou a třetí dimenzi a je znázorněn jako jednorozměrné pružné vlákno.

Již tedy víme, že gravitace je zakřivení časoprostoru. Víme také, že zakřivení je způsobeno přítomnou hmotou a že existuje mnoho obrázků, které toto vše hezky znázorňují. Hlavní otázka zní, proč vlastně hmota zakřivuje časoprostor? Mezi nejčastějšími odpověďmi najdeme, že to je přirozená vlastnost hmoty. Tomu bychom měli prostě věřit a dál se takto nevědecky neptat. Jestliže se podíváme na obrázek, je to přece na první pohled logické.

To je sice pravda, ale pouze za předpokladu, že by odněkud zdola, z pod nakreslené linky časoprostoru, působila na hmotné těleso přitažlivost. Kdyby tomu tak bylo, tak by skutečně každá hmota způsobila prohnutí, nebo chcete-li „zakřivení“ časoprostoru. Tato spekulace však vyvolává řadu dalších otázek. Odkud by se tam to gravitační pole vzalo?

I na to existují odpovědi. Víme, že gravitační síla je ekvivalentní se silou setrvačnou (jak pravil sám velký AE). Takže kdyby náš časoprostor neustále zrychloval směrem nahoru (z pohledu obr.č.2), tak by výsledný efekt byl stejný, jako kdyby odněkud zdola působilo gravitačního pole.

Tento nápad však vypadá již na první pohled nesmyslně. Představa, že existuje síla, která by byla schopna neustále urychlovat náš časoprostor někam směrem do čtvrtého prostorového rozměru se jeví velice nepravděpodobná. Než však tuto myšlenku nadobro opustíme, zkusme se na to podívat trochu jinak.

Představme si, že časoprostor kmitá střídavě nahoru a dolů. Výsledný efekt na hmotná tělesa pak bude v zásadě podobný, jako při jeho neustálém zrychlování, pouze s tím rozdílem, že zakřivení časoprostoru v okolí hmotného tělesa, vyvolané setrvačnou silou tohoto tělesa, bude střídavě směrem dolů, podruhé směrem nahoru, a mezitím nebude žádné. Dále připusťme, že nemusí naráz celý prostor kmitnout nahoru a pak zase celý kmitnout dolu, ale úplně stejný efekt bude mít sinusový průběh těchto kmitů. Tomuto střídavému pohybu časoprostoru nahoru a dolu budeme říkat vlnění časoprostoru. Mohli bychom ho nazvat třeba vibrace, nebo chvění, ale pojem vlnění je nejběžnější. Tak si představme, že se náš časoprostor vlní.

                                         
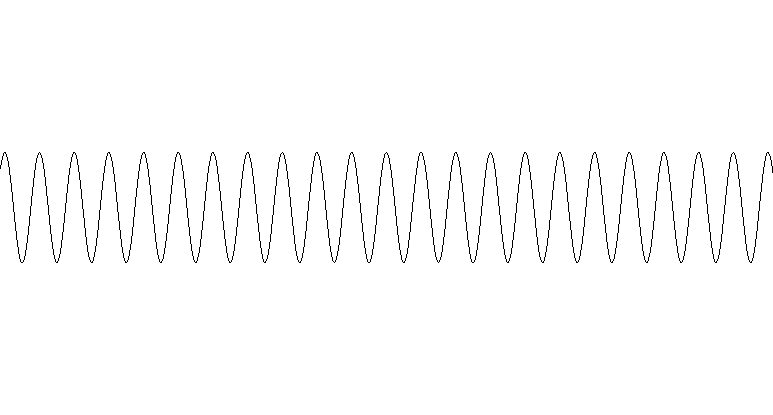
Obr. 3 – náš časoprostor znázorněný jednorozměrnou čárou se vlní

Nyní do vlnícího se prostoru umístíme hmotné těleso. Zobrazíme je jako bod, který je součástí tohoto prostoru. Stejně jako v obecně přijímané teorii ovlivňuje hmotný bod prostor kolem sebe tak, že jej zakřivuje, tak i v tomto modelu je vlnící se prostor hmotou ovlivněn. To se projevuje snížením energie vlnění v okolí hmotného tělesa. Pokles energie vlnění se může projevit buď zmenšením amplitudy (horní část obrázku 4), nebo snížením frekvence (dolní část obrázku 4). Nebo obojím.

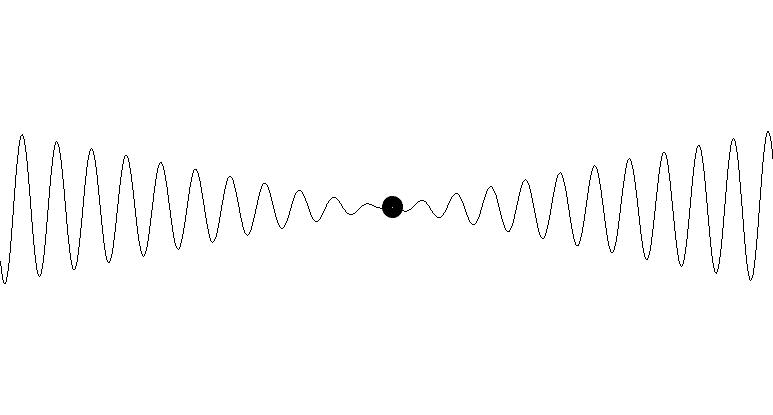
Obr. 4 – vliv hmotného tělesa na vlnění časoprostoru ve svém okolí

Lze tedy předpokládat, že dojde ke snížení frekvence vlnění. Zkusme použít jako analogii strunu hudebního nástroje. Co nastane, pokud přidáme hmotu na rezonující strunu? Struna bude vydávat hlubší tón, protože frekvence kmitání se sníží. Tato analogie nám naznačuje, jakým způsobem ovlivňuje hmotné těleso vlnění časoprostoru ve svém nejbližším okolí. To má ovšem zásadní dopad na veškeré přírodní děje probíhající v gravitačním poli.

Vlivem nižší frekvence vlnění časoprostoru dochází v okolí hmotného tělesa ke zpomalení veškerých dějů, včetně oscilace elektronů v atomových hodinách. Jednoduše řečeno – dochází ke zpomalení času. Tato skutečnost již byla mnohokrát prokázána. Opravdu již máme tak přesné hodiny, že když jedny položíme na zem a druhé zvedneme nad hlavu, tak uvidíme, že ty hořejší hodiny půjdou rychleji. Vědci umí ten časový rozdíl spočítat pomocí rovnic, ale kdybychom se jich zeptali, proč při změnách gravitačního potenciálu plyne čas jinou rychlostí, tak nám odpoví dosti neurčitě. Že to je taková vlastnost gravitace a že je to způsobeno zakřivením časoprostoru. Změna frekvence vlnění časoprostoru není mezi uznávanými teoriemi.

Pokud si alespoň jediný čtenář dokáže zpomalení času v gravitačním poli představit pomocí této analogie se snížením frekvence vlnění časoprostoru a pomůže mu to v dalším chápání dějů okolo nás, tak tento článek splnil svůj úkol.

Jestli do prostoru umístíme dvě hmotná tělesa blízko sebe, bude výsledek vypadat takto:

Obr. 5 – vliv dvou hmotných těles na vlnění časoprostoru ve svém okolí

Energie vlnění prostoru mezi hmotnými tělesy je nižší než energie vlnění vně této soustavy hmotných těles. Na tuto soustavu hmotných těles se můžeme dívat tak, že energeticky větší vlnění prostoru vně systému dvou těles „tlačí“ na tělesa a nutí je přibližovat se k sobě, jelikož vlnění mezi hmotnými tělesy je energeticky nižší. Tlakem tohoto vlnění dochází k tomu, že se hmotná tělesa k sobě budou přibližovat. dojde ke vzniku přitažlivé síly mezi těmito tělesy. Pokud přijmeme tuto hypotézu, tak zřetelně uvidíme rozdíl mezi gravitační silou a ostatními třemi přírodními silami (elektromagnetickou, silnou a slabou). Nebude zapotřebí dále hledat hypotetický graviton, přestože ostatní tři známé síly potřebují fotony, gluony a bosony ke své existenci. A také si uvědomíme, že gravitační pole nespotřebovává energii tak, jako ostatní síly, ale naopak způsobuje úbytek energie vlnění prostoru.

Einsteinova obecná teorie relativity říká, že hmota svojí přítomností zakřivuje časoprostor kolem sebe. Tato myšlenka nás svádí k představě hlubokých trychtýřů, které vytváří časoprostor v blízkosti hmotných těles, což může být zavádějící.

Na základě našich úvah a s přihlédnutím k obrázku číslo 5 můžeme nabídnout alternativní názor, že hmota způsobuje „narovnávání“ časoprostoru tím, že tlumí frekvenci a amplitudu vlnění časoprostoru ve svém okolí. Tato alternativa nám přináší jasnější představu o tom, čím je způsobeno zpomalení času v blízkosti velké hmoty.

Zajímavé možnosti nám nabízí kvantový pohled na tuto gravitační hypotézu:

Kvantový pohled na gravitaci:

Po mnoho let byl atom nedělitelnou částicí. S pokrokem vědy došlo k rozložení „nedělitelného“ atomu na elektrony a nukleony. Dnes víme, že i tyto částice sestávají z dalších, mnohem menších částic, které pravděpodobně také nejsou tou nejmenší, již doopravdy nedělitelnou částicí. Pro další úvahy si zavedeme tyto tři předpoklady:

1. dělitelnost částic je konečná, z čehož plyne, že „Nejmenší částice“ (NČ) skutečně existuje.
2. existuje pouze jeden druh NČ, ze kterého lze sestavit všechny ostatní, tedy složené částice.
3. pokud se v budoucnu ukáže, že tato NČ je dále dělitelná, tak se název „nejmenší částice“ bude nadále používat pouze pro fragmenty tohoto dělení.

Na obr.6 si znázorníme a popíšeme různé stavy, ve kterých se NČ ocitá ve vlnícím se časoprostoru:

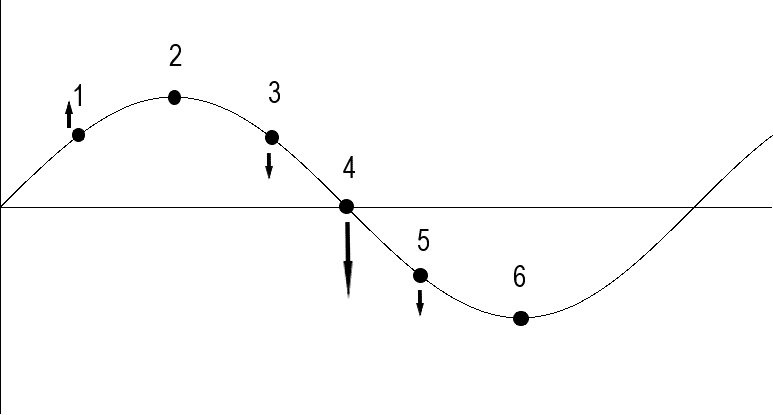
Obr. 6 – různé stavy NČ v časoprostoru – šipky znázorňují velikost a směr rychlosti jejich pohybu ve vlně

Při popisu jednotlivých stavů NČ na obr.6 si budeme všímat jejich svislého pohybu, v tuto chvíli zanedbáme jakýkoliv pohyb vodorovný. Nakreslené šipky ukazují směr a velikost rychlosti pohybu NČ. Sinusoida, která znázorňuje časoprostor, se vlní. Zde je slovní popis jednotlivých stavů NČ:

1. V tomto bodě se NČ pohybuje určitou rychlostí nahoru, která je již v této fázi časoprostorové vlny intenzivně zpomalována.
2. Zde na vrcholu vlny se svislý pohyb NČ úplně zastavil a nastává obrat, částice se za malý okamžik začne pohybovat směrem dolů. Změna rychlosti NČ je v tuto chvíli největší.
3. V bodě tři částice zrychluje směrem dolů.
4. Nyní má NČ nejvyšší vertikální rychlost, její pohyb je navíc v tomto bodě rovnoměrný. Částice dokončila zrychlování a v dalším okamžiku začne se zpomalováním.
5. V tomto bodě se opakuje děj z bodu 1. pouze s tím rozdílem, že směr rychlosti je obrácen směrem dolů.
6. A v bodě 6. nastává totéž, co v bodě 2.

Nejzajímavější fáze pohybu nastává v bodě č.4. V tomto okamžiku totiž částice nemění svoji vertikální rychlost, pohybuje se naprosto rovnoměrně. Proto tedy neovlivňuje okolní časoprostor a nemá vliv na jeho zakřivení (narovnávání). V této fázi přichází NČ o svoji hmotnou podstatu. Částice se stává pro tento okamžik nehmotnou, nepůsobí na ní žádná gravitační síla okolních částic a ani ona žádnou gravitační sílu nevytváří. Pro vnějšího pozorovatele přestává částice v tuto chvíli existovat. Naopak, pokud je částice v bodě 2. nebo 6., je její změna rychlosti nejvyšší a interakce s časoprostorem největší. Ostatní (liché) body jsou „mezi stavy“, ve kterých se částice nachází při jednotlivých změnách fáze vlnění. Pokud by se částice navíc v časoprostoru pohybovala vodorovně, vytvářela by přerušovanou stopu tak, jak by se neustále střídala její hmotná a nehmotná fáze. Stejně tak vzniká a zaniká gravitace touto částicí tvořená.

Obr. 7 – NČ při pohybu v časoprostoru střídá hmotný a nehmotný stav.

NČ se při pohybu časoprostorem navzájem ovlivňují. Vzájemná interakce mezi NČ je určována jejich vzájemnou rychlostí, vzdáleností mezi nimi a fází vlnění časoprostoru, ve které se právě nacházejí (hmotná nebo nehmotná). Za určitých předem daných podmínek budou NČ kolem sebe obíhat po stabilních drahách. Způsobů vzájemného obíhání dvou NČ může být poměrně mnoho. Ty nejjednodušší jsou znázorněny na obrázku č.8:

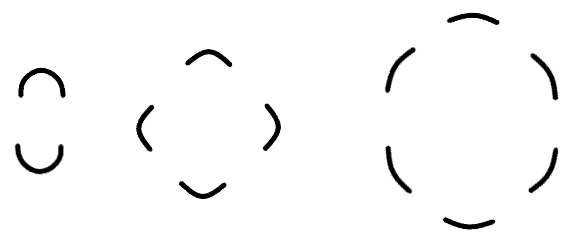
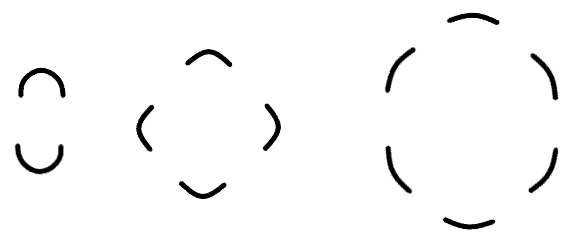
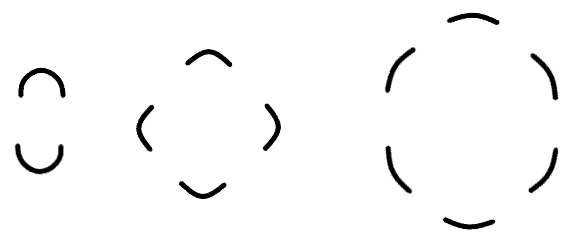
Obr. 8 – různé dráhy dvou vzájemně se obíhajících NČ, při jejichž pohybu se střídá hmotný a nehmotný stav.

Lze si představit ještě další stabilní orbity, po kterých se obíhají páry nejmenších částic. Tyto párové soustavy se mohou spolu vzájemně obíhat, čímž vytvářejí soustavy vyššího řádu. Takto vznikají více či méně stabilní částice, které nazýváme základními (elementárními). Pro zajímavost lze ještě uvést, že výsledná hmotnost složené částice neodpovídá součtu hmotností jednotlivých NČ, ale je výhradně určena tím, do jaké míry snižuje konkrétní složená částice vlnění časoprostoru ve svém okolí.

Je jasné, že pokud připustíme existenci tohoto modelu gravitace, bude to mít dalekosáhlé dopady na náš pohled na vesmír.